Top 60 Statistics & A/B Testing Interview Questions (2025)
Overview
Statistics and A/B testing interview questions are integral to data science interviews, with over 60% focusing on these to assess your fundamental data science skills.
As a data scientist, you must know that statistics serves as the backbone of data science methodologies. Your proficiency in stats enables interviewers to confidently assess your ability to analyze, interpret, and derive insights from complex datasets and build machine learning algorithms.
A/B testing interview questions and statistics are usually asked in tandem in interviews, as statistics are heavily utilized in experiment design. There are four main types of statistics and A/B questions that are asked:
Basic A/B Testing Interview Questions
In data science interviews, easy A/B testing interview questions ask for definitions, gauge your understanding of experiment design, and determine how you approach setting up an A/B test. Some of the most common basic A/B testing interview questions include:
1. What types of questions would you ask when designing an A/B test?
This type of question assesses your foundational knowledge of A/B test design. You don’t want to begin without first understanding the problem the test aims to solve. Some questions you might ask include:
- What does the sample population look like?
- Have we taken steps to ensure our control and test groups are truly randomized?
- Is this a multivariate A/B test? If so, how does that affect the significance of our results?
2. You are testing hundreds of hypotheses with many t-tests. What considerations should be made?
The most important consideration is that running multiple t-tests exponentially increases the probability of false positives (also called Type I errors).
“Exponentially” here is not a placeholder for “a lot.” If each test has false-positive probability ψ, the probability of never getting a false positive in n many tests is (1 − ψ)n, which clearly tends to zero as n→∞.
There are two main approaches to consider in this situation:
- Use a correction method such as the Bonferroni correction
- Use an F-test instead
3. How would you approach designing an A/B test? What factors would you consider?
In general, you should start with understanding what you want to measure. From there, you can begin to design and implement a test. There are four key factors to consider:
- Setting metrics: A good metric is simple, directly related to the goal at hand, and quantifiable. Every experiment should have one key metric that determines whether the experiment was successful.
- Constructing thresholds: Determine to what degree your key metric must change for the experiment to be considered successful.
- Sample size and experiment length: How large of a group will you test on, and for how long?
- Randomization and assignment: Who gets which version of the test and when? You need at least one control group and one variant group. As variants increase, the number of groups needed increases, too.
4. What are the pros and cons of a user-tied test vs. user-untied test?
It’s helpful to first explain the difference between user-tied and user-untied tests. A user-tied test is a statistical test in which the experiment buckets users into two groups on the user level. Therefore, a user-untied test is one in which they are not bucketed on the user level.
For example, in a user-untied test on a search engine, traffic is split at the search level instead of the user level, given that a search engine generally does not need you to sign in to use the product. However, the search engine still needs to A/B test different algorithms to measure better ones.
One potential con of a user-tied test is that bias can be problematic in user-untied experiments because users aren’t bucketed and can see both treatments. What are other pros and cons you can think of?
5. What p-value should you target in an A/B test?
Typically, the significance level of an experiment is 0.05, and the power is 0.8. Still, these values may shift depending on how much change needs to be detected to implement the design change. The amount of change needed can be related to external factors, such as the time needed to implement the change once the decision has been made.
A p-value of <0.05 strongly indicates that your hypothesis is correct and the results aren’t random.
6. The results of a standard control-variant A/B test have a .04 p-value. How would you assess the validity of the result?
Hint: Is the interviewer leaving out important details? Are there more assumptions you can make about the context of how the A/B test was set up and measured that will lead you to discover invalidity?
Looking at the actual measurement of the p-value, you already know that the industry standard is .05, which means that 19 out of 20 times that you perform that test, you’re going to be correct that there is a difference between the populations. However, you have to note a couple of considerations about the test in the measurement process:
- The sample size of the test
- How long it took before the product manager measured the p-value
- How the product manager measured the p-value and whether they did so by continually monitoring the test
What would you do next to assess the test’s validity?
7. What are some common reasons A/B tests fail?
There are numerous scenarios in which bucket testing won’t reach statistical significance or the results are unclear. Here are some reasons you might avoid A/B testing:
- Not enough data: A statistically significant sample size is key for an effective A/B test. If a landing page isn’t receiving enough traffic, you likely won’t have a large enough sample size for an effective test.
- Your metrics aren’t clearly defined: An A/B test is only as effective as its metrics. If you haven’t clearly defined what you’re measuring or your hypothesis can’t be quantified, your A/B test results will be unclear.
- Testing too many variables: Trying to test too many variables in a single test can lead to unclear results.
8. You’re told that an A/B test with 20 different variants has one “ significant variant.” What questions would that raise?
When you’re testing more than one variant, the probability that you reached significance on a variant by chance is high. You can understand this by calculating the probability of one significant result by taking the inverse of the p-value that you are measuring.
Therefore, if you want to know the probability of getting a significant result by chance, you can take the inverse of that. For example: P(one significant result) = 1 − P(number of significant results) = 1 − (1 − 0.05) = 0.05
There is a 5% probability of getting a significant result just by chance alone. This makes intuitive sense, given how significance works. Now, what happens when you test 20 results and get one significant variant back? What’s the likelihood it occurred by chance?
P(one significant result) = 1 − (1 − 0.05)^20 = 0.64 or a 64% chance that you got an incorrect significant result. This result is otherwise known as a false positive.
9. How long should an A/B test run?
Experiment length is a function of sample size since you’ll need enough time to run the experiment on X users per day until you reach your total sample size. However, time introduces variance into an A/B test; there may be factors present one week that aren’t present in another, like holidays or weekdays vs. weekends.
The rule of thumb is to run the experiment for about two weeks, provided you can reach your required sample size within that time. Most split tests run for 2-8 weeks. Ultimately, the length of the test depends on many factors, such as traffic volume and the variables being tested.
10. What are some alternatives to A/B testing? When is an alternative the better choice?
If you’re looking for an alternative to A/B testing, there are two common tests that are used to make UI design decisions:
- A/B/N tests: This type of test compares several versions simultaneously (the N stands for “number,” e.g., the number of variations being tested) and is best for testing major UI design choices.
- Multivariate: This type of test compares multiple variables at once, e.g., all the possible combinations that can be used. Multivariate testing saves time; you won’t have to run numerous A/B tests. This type of test is best when considering several UI design changes.
11. What’s the importance of randomization in split testing? How do you check for proper randomization?
To guarantee the validity of the A/B test results, it is important to ensure a normal distribution of users with various attributes; randomizing insufficiently may result in confounding variables later.
It also matters when A/B tests are given to users. For instance, is every new user given an A/B test? How will that affect the assessment of existing users? Conversely, if A/B tests are assigned to all users, and some of those users signed up for the website this week while others have been around for much longer, is the ratio of new users to existing users representative of the larger population of the site?
Finally, it is also important to ensure that the control and variant groups are of equal size so that they can be easily (and accurately) compared at the end of the test.
12. What metrics might you consider in an A/B test?
In general, you might consider many different metrics in an A/B test. But some of the most common are:
- Impression count
- Conversion rate
- Click-through rate (CTR)
- Button hover time
- Time spent on page
- Bounce rate
You should use the variable based on your hypothesis and what you’re testing. If you’re testing a button variation, button hover time or CTR are probably the best choices. But if you’re testing messaging choices on a long-form landing page, time spent on the page and bounce rate would likely be the best metrics to consider.
13. What are some of the common types of choices you can test with A/B testing?
In general, A/B testing works best at informing UI design changes and with promotional and messaging choices. You might consider an A/B test for:
- UI design decisions
- Testing promotions, coupons, or incentives
- Testing messaging variations (e.g., different headlines or calls-to-action)
- Funnel optimizations
14. In an A/B test, how can you check if assignment to the various buckets was truly random?
You can check for randomness by:
- Comparing baseline metrics (e.g., demographics, past behavior) across groups to ensure similarity.
- Performing a Chi-square test for categorical variables and a t-test for continuous variables.
- Checking for time-based patterns to ensure randomization wasn’t affected by external factors.
15. What are the Z and t-tests? What are they used for? What is the difference between them? When should we use one over the other?
- Z-test: Used when the population variance is known and the sample size is large (n>30n > 30n>30).
- t-test: Used when the population variance is unknown and the sample size is small (n≤30n \leq 30n≤30).
- Difference: The Z-test relies on the normal distribution, while the t-test accounts for more variability with smaller samples.
- When to use: Use a t-test for small samples and unknown variance; use a Z-test for large samples with known variance.
16. In the context of hypothesis testing, what are type I errors (type one errors) and type II errors (type two errors)? What is the difference between the two?
- Type I error (False Positive): Rejecting a true null hypothesis (detecting an effect when none exists).
- Type II error (False Negative): Failing to reject a false null hypothesis (missing a real effect).
- Key difference: Type I errors are controlled by the significance level (α\alphaα), while Type II errors depend on statistical power (beta).
Case Study A/B Testing Interview Questions
You will want to approach A/B testing case study questions with a clear understanding of the A/B test experiment design process. Consider all potential factors when designing an A/B test.
The more you can demonstrate a thorough understanding of the scope of the problem, the more suitable you’ll appear as a candidate. Some sample A/B testing case study questions include:
17. You design an A/B test to measure user response rates. The control group outperforms the treatment group. What happened?
More context: The experience measured financial rewards’ impact on users’ response rates. The treatment group with a $10 reward has a 30% response rate, while the control group with no reward has a 50% response rate. How could you improve this experimental design?
See a mock interview solution for this question:
18. How would you set up an A/B test to measure if the color (red or blue) and/or the position (top or bottom of the page) of a button will increase click-through?
In this case, the question prompts multiple changes within the experiment design. Due to the testing of two independent variables, the test will result in an interaction effect of two different variables, creating four variants:
- Red button - top of the page
- Red button - bottom of the page
- Blue button - top of the page
- Blue button -bottom of the page
The test is now multivariate. Notably, more test variants increase the variance of the results. One way to decrease these effects is to increase the length of time for the test to reach significance in order to reduce variance from day-to-day effects.
19. You’re asked to run a two-week A/B test to test an increase in pricing. How would you approach designing this test?
Follow-up question: Is an A/B test on pricing a good business decision?
A/B testing pricing generally has more downsides than upsides. One major downside is that if two users go to a pricing page, and one of them sees a product for $50/month, while the other sees one for $25/month, you risk an incentive for users to opt out of the A/B test and into another bucket, creating real statistical anomalies.
However, an even larger issue on A/B testing pricing is understanding success. When testing a discount rate on a subscription product, you want to know two things:
- Does the customer convert at a higher rate for the discount?
- Is the total lifetime value of the customer higher as well?
Running a recurring revenue A/B test means running a pricing test for at least two months: one month for all users to opt in and a second month to examine the churn rate for all initial users.
What else do you need to consider?
20. A UI test variant wins by 5% on the target metric (CVR increase). What would you expect to happen after the UI is applied to all users?
Follow-up question: Will the metric actually go up by ~5%, more, or less? You can also assume there is no novelty effect.
This question starts with numerous information gaps. Clarifying questions will help you answer more confidently. Some questions to consider asking are:
- How long did the test run for?
- What are the confidence intervals for the test?
- Is there an impact analysis or assumptions of heterogeneity on the users?
- Is the A/B test sample population a representative sample of the whole?
- Are there any interactions with other experiments?
21. How would you determine if an A/B test with unbalanced sample sizes would result in bias?
More context: One variant in the test has a sample size of 50,000 users, whereas the other has 200,000 users. Would the test result be biased toward the smaller group?
In this case, the interviewer is trying to assess how you would approach the problem given an unbalanced group. Since you are not given context to the situation, you must state assumptions or ask clarifying questions.
How long has the A/B test been running? Have they been running for the same duration? If the data was collected during different time periods, then bias certainly exists from one group collecting data from a different time period than the other.
22. How would you make a control group and test group to account for network effects?
Specifically, you want to create control and test groups to test the close friends feature on Instagram stories.
Let’s say you want to run the experiment with a per-user assignment. Half of the users in this experiment would get the close friends feature, and half would not. To further define what it means to get the close friends feature, you would say that the users would be able to create close friend stories and see close friends’ stories on Instagram.
However, this in itself presents the problem of the per-user assignment:
- Test group user creates a story - What does the control group friend see?
- Control group watches stories - What happens to all of their friends’ stories in the close friends variant?
- Test group user does not create a story - How do you analyze this effect on the friends that were not in this variant?
Per-user assignment fails many times in this scenario because you encounter network effects where you cannot properly hold one variable constant and test for the effect.
23. You run an A/B test for Uber Fleet and find the distribution is abnormal. How would you determine which variant won?
Understanding whether your data abides by or violates a normal distribution is an important first step in your subsequent data analysis. This understanding will change which statistical tests you use if you need to look for statistical significance immediately.
For example, you cannot run a t-test if your distribution is non-normal since this test uses the mean/average to find differences between groups. If you find out that the distribution of the data is not normal, there are several steps you can take to help fix this problem:
- Perform a Mann-Whitney U-Test
- Utilize bootstrapping
- Gather more data
24. How would you infer whether the results of an A/B test of click-through rates were statistically significant?
With this question, you should start with some follow-up clarifying questions like:
- How were the control and variant groups sampled?
- Was it a random sample, and was it done by following the agreed-upon test conditions?
- Is the time frame of the data for both groups the same, and did you follow the agreed-upon duration to run the analysis?
- What does the distribution of data for the two groups look like?
- Is the data normally distributed for both controlled and variant groups?
Once you’ve obtained clarity, you can calculate the p-value or find the rejection region to determine if you should reject or fail to reject a null hypothesis.
25. How would you evaluate if displaying free shipping on the checkout page will lead to more conversions?
Let’s say you work at an e-commerce startup. You run an A/B test on the company’s checkout product page, hypothesizing that free shipping will increase conversions.
The experiment group specifies whether the product qualifies for free shipping. The control group does not specify free shipping.
Let’s say we run the experiment for two weeks and get these results.
Control:
- 3056 page visits
- 1413 conversions
- 46% conversion
Experiment:
- 2947 samples
- 1533 conversions
- 52% conversion
How would you evaluate the results and whether the test was successful?
26. How do we go about selecting the best 10,000 customers for the pre-launch?
Context:
Let’s say that you are working as a data scientist at Amazon Prime Video, and they are about to launch a new show but first want to test the launch on only 10,000 customers first
How do we go about selecting the best 10,000 customers for the pre-launch?
What would the process look like for pre-launching the TV show on Amazon Prime to measure how it performs?
To select the best 10,000 customers, prioritize engaged users based on past streaming behavior, genre preferences, and likelihood to provide meaningful feedback. Use customer segmentation, churn probability models, and machine learning techniques to identify the most relevant audience. The pre-launch process should include A/B testing different promotional strategies, monitoring key performance metrics (watch time, engagement, retention), and gathering qualitative feedback to refine marketing and content strategies before a full release.
27. How would you determine if a redesigned email campaign caused a conversion rate increase rather than other factors?
To isolate the impact of the redesigned email campaign, analyze historical trends to rule out external factors like seasonality or marketing changes. Conduct an A/B test comparing users exposed to the new vs. old email journey. Use statistical tests (e.g., t-test) to assess significance and ensure the increase isn’t due to random fluctuations. Additionally, control for variables such as user demographics, traffic sources, and market trends to validate the campaign’s causal impact.
28. Your manager ran an A/B test with 20 variants and found one significant. Would you question the results?
Finding one significant result among 20 variants raises concerns about multiple testing errors (false positives). To verify validity, apply statistical corrections like the Bonferroni adjustment or False Discovery Rate control. Check if the effect size is meaningful and whether results replicate in a follow-up test. Consider running a holdout validation or Bayesian analysis to confirm the true impact of the variant before making business decisions.
Basic Statistics Interview Questions
Basic statistics interview questions to filter out candidates without a firm technical grasp of statistics and who struggle to communicate their findings to others.
You might also be asked to describe the difference between Type I (false positive) and Type II (false negative) errors, as well as how to go about detecting them, or to describe what a result with a significance level of 0.05 actually means.
If you’re familiar with the statistical concepts relevant to your job as a data scientist, this part of the interview should be pretty straightforward. Some conceptual statistics interview questions include:
29. What is a null hypothesis?
The null hypothesis suggests that there is no statistically significant relationship between the two sets of data. For example, if you were comparing weight loss between a keto and a low-carb diet, the null hypothesis would be that there is no statistical difference in the mean weight loss amount between the two diets.
30. How would you explain p-value to someone who is unfamiliar with the term?
An interviewer is looking for whether you can answer this question in a way that conveys both your understanding of statistics and your ability to explain this concept to a non-technical worker.
Use an example to illustrate your answer:
Say we’re conducting an A/B test of an ad campaign. In this type of test, you have two hypotheses. The null hypothesis states that the ad campaign will not have a measurable increase in daily active users. The test hypothesis states that the ad campaign will have a measurable increase in daily active users.
Then, data will be used to run a statistical test to determine which hypothesis is true. The p-value can help determine this by providing the probability of whether you would observe the current data if the null hypothesis were true. Note, this is just a statement about probability given an assumption; the p-value is not a measure of “how likely” the null hypothesis is to be right, nor does it measure “how likely” the observations in the data are due to random chance, which are the most common misinterpretations of what the p-value is. The only thing the p-value can say is how likely you are to get the data you got if the null hypothesis were true. The difference may seem very abstract and impractical, but using incorrect explanations contributes to the overvaluing of p-values in non-technical circles.
Therefore, a low p-value indicates that it would be extremely unlikely that the data would result in this way if the null hypothesis were true.
31. What are the primacy and novelty effects?
The primacy effect involves users resisting change, whereas the novelty effect involves users becoming temporarily excited by new things. For example, Instagram launched a new feature called close friend stories. Users could be drawn to this new feature because it’s new, but after using it for a while, they might lose interest and use it less.
32. What are Type I and Type II errors?
A Type I error is a false positive or rejecting a true null hypothesis. A Type II error is a false negative or the failure to reject a true null hypothesis.
33. What is the difference between covariance and correlation? Provide an example.
Hint: What values can covariance take? What about correlation? The difference between covariance and correlation is that covariance can take on any numeric value, whereas correlation can only take on values between −1 and 1.
34. What is a holdback experiment?
A holdback experiment rolls out a feature to a high proportion of users. Still, it holds back the remaining percentage of users to monitor their behavior over a longer period of time. This allows analysts to quantify a change’s “ lift ” over a longer time.
35. What is an unbiased estimator, and can you provide an example for a layman to understand?
Hint: What would a biased estimator look like? How does an unbiased estimator differ?
The key here is explaining this concept in layman’s terms. An unbiased estimator is an accurate statistic used to approximate a population parameter. A statistic, in this case, would be a piece of data that defines a population in some way, such as the mean and median of a population.
To further simplify, approximating a population parameter means using this estimator, or statistic, to measure the same statistic on the entire population effectively. If you use the mean as an example, then the unbiased estimator is the sample mean being equivalent to the population mean. If you overestimate or underestimate the mean value, then the mean of the difference between the sample mean and the population mean is the bias.
Now, go into the layman’s example by painting a picture for the interviewer. You want to figure out how many people will vote for the Democratic or Republican presidential candidate. You can’t survey the entire eligible voting population of over 100 million, so you sample around 10,000 people over the phone. You find out that 50% will vote for the Democratic presidential candidate. Is this an unbiased estimator?
36. What is the Central Limit Theorem?
The central limit theorem says that if there is a very large sample of independent variables, they will eventually become normally distributed.
37. What is a normal distribution?
Most people probably recognize this graph as the ordinary bell curve distribution, in which the relevant features of a given group are evenly distributed around the curve’s mean.
38. What are time series models? Why do we need them when we have less complicated regression models?
You need time series models because of a fundamental assumption of most standard regression models: no autocorrelation. In layman’s terms, this means that a data point’s values in the present are not influenced by the values of data points in the past.
39. What do the AR and MA components of ARIMA models refer to? How do you determine their order?
The AR component stands for autoregression, in which the value of a current data point is determined in part by the value of a previous data point. The MA component stands for moving average, in which the mean of the random noise of a random process changes over time.
ARIMA models contain both an autoregressive and a moving average component. Current data points are assumed to result from the last p data points and last q errors, along with some random noise.
40. How would you interpret coefficients of logistic regression for categorical and boolean variables?
Boolean variables have values of 0 or 1. Examples include gender, whether someone is employed, and whether something is gray or white.
The sign of the coefficient is important. If you have a positive sign on the coefficient, then that means that all else is equal, and the variable has a higher likelihood of positively influencing the outcome variable. Conversely, a negative sign implies an inverse relationship between the variable and the outcome you are interested in. Further, if the value for the Boolean variable is 1, the effect is counted toward the outcome. If the value is 0, the effect is diminished with respect to the outcome variable.
41. What’s the difference between MLE vs MAP
Maximum likelihood estimation (MLE) and maximum posterior (MAP) are methods used to estimate a variable with respect to observed data. They are both good for estimating a single variable instead of a distribution.
If you get into the math between the two methods, one distinct difference between the two is the inclusion of the prior assumption of the model parameter in MAP. Otherwise, they are essentially identical. This added parameter means that the likelihood is weighted with some weight on the prior. Thus, the two methods can be used to estimate parameters but have slightly different approaches to achieving them.
Probability and Statistics Practice Problems
In statistics interviews for data science positions, you’ll likely be asked computational questions or provided case studies, testing your knowledge of statistics and probability.
When answering this type of question, make sure that you present a solution to the problem at hand and walk the interviewer through the thought process you used when arriving at your answer.
Cite any relevant statistical concepts employed in your solution and make your response as intelligible as possible for the layperson. Here are some sample statistics case study interview questions:
42. Given uniform distributions X and Y and the mean 0 and standard deviation 1 for both, what’s the probability of 2X > Y?
Hint: Given that X and Y both have a mean of 0 and a standard deviation of 1, what does that indicate for the distributions of X and Y? What are some of the scenarios you can imagine when you randomly sample from each distribution? Detail each of the possibilities where X > Y and X < Y, as well as possible values of X and Y in each.
43. Given X and Y are independent variables with normal distributions, what is the mean and variance of the distribution of 2X − Y when the corresponding distributions are X ~ N (3, 2²) and Y ~ N(1, 2²)?
The linear combination of two independent normal random variables is a normal random variable itself. How does this change how you solve for the mean of 2X − Y?
Hint: The variance of aX − bY depends on the constants a and b, Var(X)/Var(Y), and Cov(X,Y). If you know that between independent random variables, the covariance equals 0, how can you use this information for computing the variance?
44. Let’s say you have a sample size of N. The margin of error for the sample size is 3. How many more samples do you need to decrease the margin of error to 0.3?
Recall the equation:
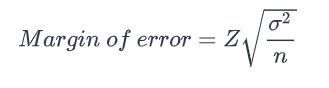
Hint: To decrease the margin of error, you will probably have to increase the sample size. But by how much?
45. You’re given a fair coin. You flip the coin until either Heads Heads Tails (HHT) or Heads Tails Tails (HTT) appears. Is one more likely to appear first? If so, which one and with what probability?
Hint: What do the two sequences, HHT and HTT, have in common? Since the question asks you to flip a fair coin until one of the two sequences comes up, it may be useful to consider the problem given a larger sample space. What happens to the probability of each sequence appearing as you flip the coin four times? Five times? N times?
46. Three zebras are chilling in the desert when a lion suddenly attacks. Each zebra is sitting on a corner of an equal length triangle and randomly picks a direction to run along the outline of the triangle to either edge of the triangle. What is the probability that none of the zebras will collide?
Hint: How many scenarios are there in which none of the zebras collide? There are two scenarios in which the zebras do not collide: if they all move clockwise or if they all move counterclockwise. How do you calculate the probability that an individual zebra chooses to move clockwise or counterclockwise? How can you use this individual probability to calculate the probability that all zebras choose to move in the same direction?
47. Let’s say that you’re drawing N cards from a deck of 52 cards. How do you compute the probability that you will get a pair from your hand of N cards?
Hint: What’s the probability of never drawing a pair?
48. What do you think the distribution of time spent per day on Facebook looks like? What metrics would you use to describe that distribution?
Having the vocabulary to describe a distribution is an important skill when it comes to communicating statistical ideas. There are four important concepts, with supporting vocabulary, that you can use to structure your answer to a question like this:
- Center (mean, median, mode)
- Spread (standard deviation, interquartile range, range)
- Shape (skewness, kurtosis, uni- or bimodal)
- Outliers (do they exist?)
In terms of the distribution of time spent per day on Facebook, you can imagine there may be two groups of people on Facebook: a) people who scroll quickly through their feed and don’t spend too much time on Facebook, and b) people who spend a large amount of their social media time on Facebook. Therefore, how could you describe the distribution using the four terms listed above?
49. Let’s say you’re trying to calculate churn for a subscription product. You noticed that out of all the customers who bought subscriptions in January 2020, about 10% of them canceled their membership before their next cycle on February 1st. How do you extrapolate this knowledge to determine the overall churn for the product?
If you assume that your new customer acquisition is uniform throughout each month and that customer churn goes down by 20% month over month, what’s the expected churn for March 1st out of all customers that bought in January?
50. Imagine a randomly shuffled deck of 500 cards numbered from 1 to 500. If you’re asked to pick three cards, one at a time, what’s the probability of each subsequent card being larger than the previously drawn card?
Hint: What if the question is actually 100 cards and you select 3 cards without replacement? Does the answer change?
51. Given N samples from a uniform distribution [0, d], how would you estimate?
A uniform distribution is a straight line over the range of values from 0 to d, where any value between 0 to d is equally likely to be randomly sampled.
So, practically, if you have N samples and you have to estimate what d is with zero context of statistics and based on intuition, what value would you choose?
For example, if the N sample is 5 and the values are (1,4,6,2,3), what value would you guess as d? Is it the max value of 6?
52. Can you calculate the t-value and degrees of freedom of a test given the following parameters?
More context: Let’s say you manage products for an e-commerce store. You think products from Category 9 have a lower average price than those in all other categories.
Here’s a short solution using SQL:
WITH CTE_1 as -- CTE_1 to calculate mean, n, variance
(
SELECT * FROM
(SELECT AVG(price) AS mean_1, count(*) AS n_1, VAR_SAMP(price) AS var_1 FROM products WHERE category_id = 9 ) x
JOIN
(SELECT AVG(price) as mean_2, count(*) AS n_2, VAR_SAMP(price) AS var_2 FROM products WHERE category_id <> 9 ) y
ON 1 = 1
),
CTE_2 -- and power(var,2)/n
AS
(
SELECT *,POWER(var_1,2)/n_1 as X_1, POWER(var_2,2)/n_2 AS X_2 FROM CTE_1
)
SELECT -- Calculate T_value and D_o_F (Welch formula)
CAST((mean_1-mean_2)/sqrt((var_1/n_1)+(var_2/n_2)) AS DECIMAL(10,5)) AS t_value,
FLOOR((POWER((X_1+X_2),2))/((POWER(X_1,2))/(n_1-1) + (POWER(X_2,2))/(n_2-1))) as d_o_f
from CTE_2
53. What could be the cause of capital approval rates going down?
More context: Capital approval rates have gone down. Let’s say last week it was 85%, and the approval rate went down to 82% this week, which is a statistically significant reduction. The first analysis shows that all approval rates stayed flat or increased over time when looking at the individual products:
- Product 1: 84% to 85% week over week
- Product 2: 77% to 77% week over week
- Product 3: 81% to 82% week over week
- Product 4: 88% to 88% week over week
What could be the cause of the decrease?
This is an example of Simpson’s paradox, which is a phenomenon in statistics and probability. Simpson’s Paradox occurs when a trend shows in several groups but either disappears or is reversed when combining the data.
In this specific example, each product’s approval rates are binomially distributed with count ni and probability pi. The mean for each distribution would be ni x pi.
54. Let’s say you’re working with survey data sent in the form of multiple-choice questions. How would you test if survey responses were filled randomly by certain individuals, as opposed to truthful selections?
Hint: Visualize survey completion times and answer patterns to distinguish random survey responses from truthful ones. If the completion time distribution is bimodal, it might suggest two groups—one responding truthfully and the other randomly. Additionally, if certain answer choices are consistently favored, especially in an unexpected pattern, this could indicate random selections. Analyzing these distributions allows you to identify the characteristics that set random responses apart from thoughtful ones.
55. What are the benefits of dynamic pricing, and how can you estimate supply and demand in this context?
Hint: To optimize dynamic pricing, estimate demand using historical data and factors like time, weather, and events while monitoring real-time supply. Price elasticity models help understand how price changes impact demand. Combining these methods allows for precise price adjustments, maximizing revenue, and balancing supply with demand.
57. Given a biased coin with probability ppp of landing heads, how can you generate a fair coin flip using this biased coin?
Hint: The key is to use sequences of flips:
- Flip the coin twice.
- If the outcome is HT, assign “heads”; if TH, assign “tails”.
- Ignore HH and TT (reroll).
This method works because HT and TH are equally likely regardless of ppp, ensuring fairness.
58. You roll two six-sided dice. What is the probability that the sum is a prime number?
Hint:
- List all possible sums: {2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}.
- Identify the prime sums: {2, 3, 5, 7, 11}.
- Count how many ways each prime sum occurs.
- Divide by the total number of outcomes (6 × 6 = 36).
60. A factory produces 5% defective items. If you randomly pick 10 items, what is the probability that at least one is defective?
Hint:
Use the complement rule: P(at least one defective)=1−P(none defective)
P(at least one defective)=1−P(none defective)P(\text{at least one defective}) = 1 - P(\text{none defective})
Each item is not defective with probability 0.95.
Since picks are independent,P(none defective)=(0.95)10
P(none defective)=(0.95)10P(\text{none defective}) = (0.95)^{10}
Subtract this from 1 to get the final answer.
Where statistics are theoretical, A/B testing mirrors real-world scenarios where businesses optimize user experiences or marketing strategies. These A/B testing interview questions will assess your approach to using A/B testing data to inform product and business decisions. Build your confidence by exploring our Statistics & AB Testing Learning Path and refining your approach with the AI Interviewer.


